1. Definición
Cuando a un objeto se le aplica una fuente luminosa éste genera una sombra,
entre el objeto y su sombra existe una relación biunívoca, de manera que a
cada punto del objeto le corresponde otro en su sombra y viceversa. Así
pues se ha establecido una relación de transformación.
"Una transformación geométrica es una operación o la combinación de
varias de ellas, en que se parte de una forma original para generar otra
nueva estableciendo una relación biunívoca entre ellas."
Transformación geométrica es una aplicación del plano en el plano tal
que a cada punto de un plano le hace corresponder otro punto del
mismo plano.
4. Clasificación
Clasificación en función al aspecto de la figura homóloga:
4.1 Isométricas: Son aquellas que conservan las
dimensiones y los ángulos entre la figura original
y la transformada.
- Traslación.
- Giro.
- Simetría.
4.2 Isomórficas: Son aquellas transformaciones
que conservan la forma, es decir, los ángulos
de la figura original y la transformada son iguales
y las longitudes son proporcionales.
- Homotecia.
- Semejanza.
4.3 Anamórficas: Son aquellas en las que cambia la
forma entre la original y la transformada.
Transformaciones geométricas
isométricas
En geometría, las transformaciones isométricas son
transformaciones de figuras en el plano que se realizan
sin variar las dimensiones ni el área de las mismas;
la figura inicial y la final son semejantes y
geométricamente congruentes. La palabra isometría
tiene su origen en el griego iso (igual o mismo)
y metria (medir), una definición cercana es igual medida.
1. Clasificación
1.1 Traslación:
La traslación es una isometría que realiza un cambio
de posición, un cambio de lugar, determinada por un
vector. Se llama traslación de vector a la isometría
que a cada punto A del plano le hace corresponder un
punto A' del mismo plano tal que AA' es igual a U (vector guía).
Las traslaciones están marcadas por tres elementos:
- La dirección, si es horizontal, vertical,
- oblicua, etc...
- El sentido, si es derecha, izquierda, arriba o
- abajo.
- La magnitud, que se refiere a cuanto se
- desplazó la figura en una unidad de medida.






Ejemplo:






Traslación de una recta

Una recta se transforma, mediante una traslación,
en una recta paralela.
en una recta paralela.
Ejercicios
 .
.1 Hallar la imagen por dicha traslación de un punto A (1,3).
2 Hallar la transformada de una circunferencia que tiene de







 , un punto
, un punto 2 La transformada de una circunferencia de










 . Hallar
. Hallar 










Composición de traslaciones

1.2 Giro:
Una rotación, en geometría, es un movimiento de cambio
de orientación de un cuerpo, de forma que dado un punto
cualquiera del mismo, éste permanece a una distancia
constante de un punto fijo, y posee las siguientes características:
- Un punto denominado centro de rotación.
- Un ángulo.
- Un sentido de rotación.
Estas transformaciones pueden ser positivas o negativas,
dependiendo del sentido de giro. Para el primer caso debe
ser un giro en sentido contrario a las manecillas del reloj,
y será negativo cuando sea en sentido de las manecillas.

1.3 Simetría:
Es la correspondencia exacta en la disposición regular de las partes o
puntos de un cuerpo o figura con relación a un punto (centro), una recta
(eje) o un plano.
¿Cómo lo puedo hacer yo solo?
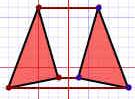
| Hazlo paso a paso. A cada esquina de la figura: | |||
| 1. Mide desde el punto de la línea de reflexión (con una línea que llegue en ángulo recto) | 2. Mide la misma distancia en el otro lado y marca un punto allí. | 3. ¡Conecta todos los puntos nuevos! | |
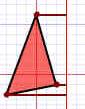 | 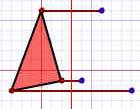 |  | |
Nombres
| Lo normal es nombrar cada esquina con una letra, y usar una pequeña raya (llamada prima) para marcar las esquinas reflejadas. Aquí, el original es ABC y la imagen reflejada es A'B'C' | 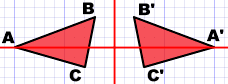 |
Algunos trucos
Eje XSi la línea de reflexión es el eje X,sólo cambia (x,y) por (x,-y) |
Eje YSi la línea de reflexión es el eje Y, cambia (x,y) por (-x,y) | 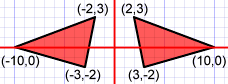 |
Doblando papelSimetría centralla línea de reflexión y mirar a través del papel!Simetría central es una transformación en la que a cada punto se le asocia otro punto que debe cumplir las siguientes condiciones:
|


Respuestas: Son simétricas.
Simetría central en O (siguiente figura).
Un giro en O se produce correspondencia de puntos.
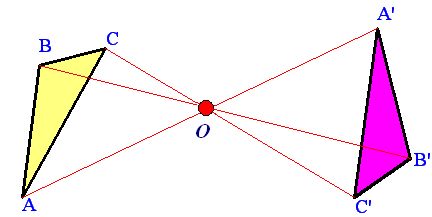
El punto O es el punto medio de las rectas que unen los
puntos homólogos.
- La simetría axial es una transformación
- respecto de un eje de simetría en la cual a cada
- punto de una figura se asocia a otro punto llamado
- imagen, que cumple con las siguientes condiciones:
- La distancia de un punto y su imagen al eje de
- simetría, es la misma.
- El segmento que une un punto con su imagen,
- es perpendicular al eje de simetría.

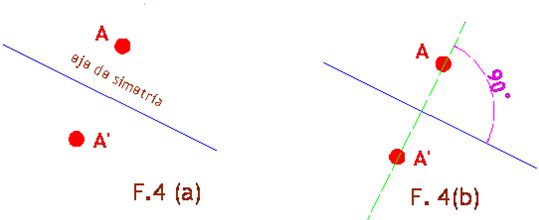
La recta (en color verde) que pasa por los puntos A y A’ es
perpendicular al eje de simetría y dichos puntos equidistan del eje.
Aplicamos el eje de simetría a un triángulo:
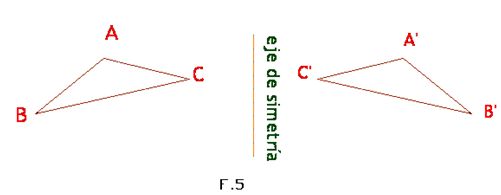
Comprobarás que ambas figuras son equidistantes respecto
al eje de simetría y que si doblaras un papel que contuviese
la F.5 por el eje de simetría, ambas figuras coincidirían.
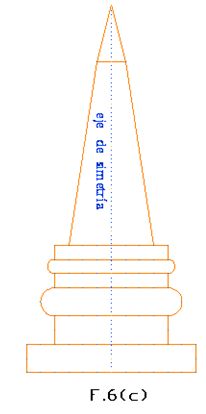
Aplicamos el eje de simetría para realizar una figura que
incluya varias líneas tal como puedes ver en F.6 (a)
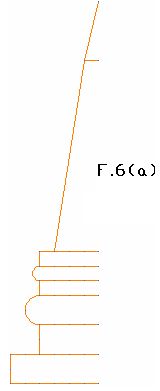
Primero dibujamos la mitad de la figura, no hace falta
dibujarla toda.
Luego trazamos el eje de simetría tal como tienes en la
F.6 (b) con la figura simétrica a F.6 (a).
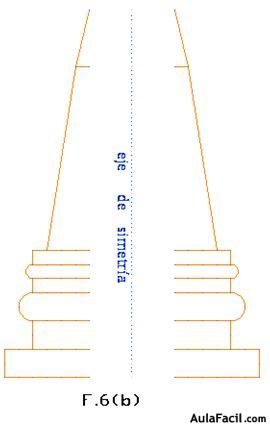
Puedes ver que hay una distancia entre ambas. Equidistan del eje de simetría
F.6 (b).
Si anulamos la distancia entre ambas figuras homólogas,
obtendremos la figura completa F.6 (c)
- Inversión.
Transformaciones geométricas isomórficas
En geometría las transformaciones geométricas - isomórficas son aquellas que solo conservan la
- forma; es decir, en ellas los ángulos de la figura
- original y de la transformada son iguales y las
- longitudes proporcionales.1. Clasificación1.1 SemejanzaDos figuras son semejantes cuando tienen la
- misma forma (el mismo número de lados y
- ángulos iguales) y distinto tamaño
- (sus dimensiones son distintas).Los diversos elementos que en las figuras
- semejantes se corresponden son proporcionales
- entre sí, existiendo igualdad entre sus ángulos.Esta correspondencia se denomina Razón de
- Semejanza (K) y es la relación de proporcionalidad
- constante que existe entre los elementos de las
- dos figuras semejantes.
 2. HomoteciaLa Homotecia es una transformación geométrica,
2. HomoteciaLa Homotecia es una transformación geométrica, - una correspondencia entre dos figuras en la que
- se cumple que las parejas de puntos homotéticos
- están alineados con el centro de homotecia O y los segmentos homotéticos son paralelos.
- Homotecia Directa: Cuando los dos puntos
- homotéticos se encuentran al mismo lado
- respecto al centro, la homotecia es directa.
- Las figuras homotéticas directas son
- semejantes y nunca son equivalentes.
 HOMOTECIA.Se llama homotecia a la transformación geométrica que
HOMOTECIA.Se llama homotecia a la transformación geométrica que - sufre una figura. A partir de un determinado punto, todas
- las medidas quedan multiplicadas por un mismo factor
- distinto de cero.En la figura F.7 tienes unos ejes de coordenadas.
- El triángulo ABC tiene sus vértices en los puntos
- A(– 2,3), B(4,2) y C(1,2).Multiplicamos a las coordenadas de cada punto por
- el factor 2 cuyos valores se transforman en:
- A’(– 4,6), B’(8,4) y C’(2,4).
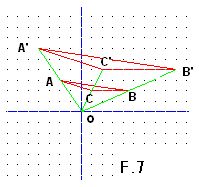 El centro de homotecia la hemos situado en O
El centro de homotecia la hemos situado en O - que corresponde a (0,0) del eje de coordenadas.En F.8 los valores de los puntos de los vértices del
- triángulo ABC son A(3,0), B(4,1) y C(2,4).El factor es 2 por lo que los vértices del triángulo
- A’B’C’ serán:(6,0), (8,2) y (4,8) respectivamente.
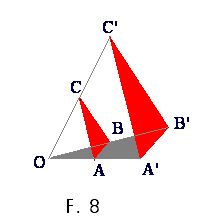 Al unir los vértices de figuras homotéticas con rectas,
Al unir los vértices de figuras homotéticas con rectas, - éstas se juntan en un punto llamado centro de homotecia
- (en los ejemplos anteriores y los próximos quedan s
- eñalados con la letra O).En la homotecia tenemos en cuenta la figura original y la homotética, ambas tendrán la misma forma pero sus
- tamaños serán diferentes dependiendo del factor o
- razón de homotecia (generalmente se le representa
- con la consonante k) si es mayor o menor que la unidad.
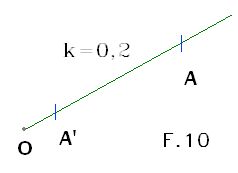
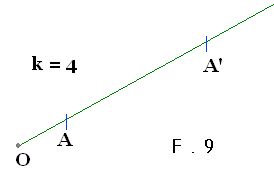 En la figura 9 vemos que no ha habido ninguna modificación de tamaño ya que estamos tratando un punto (A) pero sí tenemos una modificación de distancia:
En la figura 9 vemos que no ha habido ninguna modificación de tamaño ya que estamos tratando un punto (A) pero sí tenemos una modificación de distancia: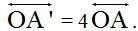 En este ejemplo A’ es homólogo de A.Si el factor k es menor que la unidad tal como lo tienes en F.10, el punto A’ queda situado entre el origen O y el punto A. La distancia OA’ vale
En este ejemplo A’ es homólogo de A.Si el factor k es menor que la unidad tal como lo tienes en F.10, el punto A’ queda situado entre el origen O y el punto A. La distancia OA’ vale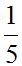 de la distancia OA
de la distancia OA 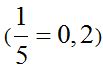 :
: 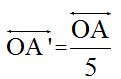
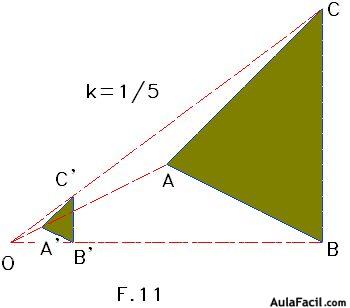
 Lo mismo sucede con las figuras homotéticas cuando
Lo mismo sucede con las figuras homotéticas cuando - k es menor que la unidad.En la F. 11 ves que el triángulo A’B’C’ queda entre el
- centro de la homotecia O y el triángulo ABC.
 ¿Qué sucede cuando k<0?En este caso nos referimos a que el valor del factor
¿Qué sucede cuando k<0?En este caso nos referimos a que el valor del factor - sea negativo.Nos fijamos en la figura 12.
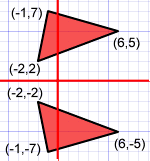
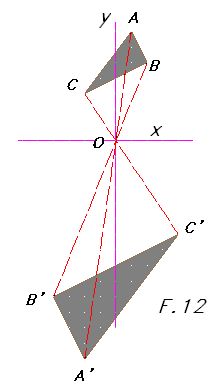 Tenemos un eje de coordenadas. Las coordenadas del punto A son (1,7), B(2,5) y C(– 2,3).La razón de homotecia o k = – 2.Las coordenadas de A’ son (4, –6), B’(–4, –10) y
Tenemos un eje de coordenadas. Las coordenadas del punto A son (1,7), B(2,5) y C(– 2,3).La razón de homotecia o k = – 2.Las coordenadas de A’ son (4, –6), B’(–4, –10) y - C’(–4, –14).Al unir con líneas discontinuas (en rojo) AA’, BB’ y
- CC’vemos el centro de homotecia O y lo que es másimportante, se produce una figura mayor e inversa.El triángulo A’B’C’ es mayor e inverso respecto del t
- riángulo ABC.
- Homotecia Inversa: Cuando los puntos
- homotéticos se encuentran alineados con
- el centro pero en extremos opuestos de las
- radiaciones, la homotecia es inversa.
- En este caso la figura no es semejante,
- es el producto de dos simetrías axiales
- cuyos ejes, uno vertical y otro horizontal,
- pasan por el centro de homotecia.

- Factor de proporcionalidad en la Homotecia:
- El factor de proporcionalidad o razón de
- semejanza entre figuras homotéticas directas
- es siempre positiva. Las figuras homotéticas
- inversas responden a un factor de proporcionalidad negativo, son equivalentes si el factor de proporcionalidad es-1.

Transformaciones geométricasan anamórficas
Son aquellas en las que cambia la forma entre la original y la transformada.Podemos distinguir tres tipos de transformación:1. HomologíaLa homología es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de las figuras. Transforma los puntos del plano A, B, C… en puntos del plano A’, B’, C’... de modo que:- Dos puntos homólogos A y A’ están alineados con un punto fijo O que es el centro de la homología.
- Dos rectas homólogas r y r’ se cortan en una recta llamada eje de homología.
 2. AfinidadLa afinidad es una homología con el centro en el infinito. Es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de la figura que transforma.Transforma los puntos del plano A, B, C… en puntos del plano A’, B’, C’... de modo que:
2. AfinidadLa afinidad es una homología con el centro en el infinito. Es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de la figura que transforma.Transforma los puntos del plano A, B, C… en puntos del plano A’, B’, C’... de modo que:- Dos puntos homólogos A y A’ definen un segmento paralelo a la dirección de afinidad d.
- Dos rectas homólogas r y r’ se cortan en una recta llamada eje de afinidad.
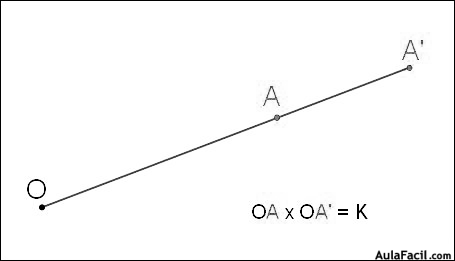
 3. InversiónLa inversión es una transformación que hace corresponder a un punto A otro punto A’ cumpliendo las siguientes condiciones:
3. InversiónLa inversión es una transformación que hace corresponder a un punto A otro punto A’ cumpliendo las siguientes condiciones:- Ambos puntos están alineados con otro punto fijo O, llamado centro de inversión.
- El producto de las distancias de ambos puntos al citado centro de inversión es un valor constante K llamado potencia de inversión, es decir; OA x OA’=K