GEOMETRIA DE SEGUNDO

• Historia de la geometría                                        Autor: Icarito


La palabra geometría está formada por las raíces griegas: "geo", tierra, y "metrón", medida, por lo tanto, su significado es "medida de la tierra".


Origen y desarrollo de la geometría

El ser humano necesitó contar, y creó los números; quiso hacer cálculos, y definió las operaciones; hizo relaciones, y determinó las propiedades numéricas.

Por medio de lo anterior, más el uso de la lógica, obtuvo los instrumentos adecuados para resolver las situaciones problemáticas surgidas a diario.

Además de esos requerimientos prácticos, el hombre precisó admirar la belleza de la creación para satisfacer su espíritu. Con ese fin, observó la naturaleza y todo lo que le rodeaba. Así fue ideando conceptos de formas, figuras, cuerpos, líneas, los que dieron origen a la parte de la matemática que designamos con el nombre de geometría.

El río Nilo

Según lo registra la historia, los conceptos geométricos que el hombre ideó para explicarse la naturaleza nacieron, en forma práctica, a orillas del río Nilo, en el antiguo Egipto.

Las principales causas fueron tener que remarcar los límites de los terrenos ribereños y construir diques paralelos para encauzar sus aguas. Esto, debido a los desbordes que causaban las inundaciones periódicas.

El aporte griego

Quienes dieron carácter científico a la geometría fueron los griegos, al incorporar demostraciones en base a razonamientos.

Tales de Mileto (600 a.C.) inició esta tendencia, al concebir la posibilidad de explicar diferentes principios geométricos a partir de verdades simples y evidentes.

Euclides (200 a.C.) le dio su máximo esplendor a esta corriente científica. Recogió los fundamentos de la geometría y de la matemática griega en su tratado Elementos.


La Geometría trata sobre las formas y sus propiedades.
Los dos temas más comunes son:

	Geometría Plana (sobre formas planas como líneas rectas, círculos y triángulos... formas que se pueden dibujar en un trozo de papel)
	Geometría Sólida (sobre objetos tridimensionales como cubos y pirámides).

Si te gusta jugar con objetos, o te gusta dibujar, ¡la geometría es para ti!

Pista: Intenta dibujar algunas de las formas y ángulos en el momento en que los aprendes... eso ayuda.

¡Sólidos!

La Geometría Sólida es la geometría del espacio tridimensional, el tipo de espacio donde vivimos...

	Poliedros: (deben tener caras planas)	Sólidos Platónicos Prismas Pirámides
	No Poliedros: (si alguna superficie no es plana)	Esfera Toro Cilindro Cono

Conceptos básicos

Para el estudio de la geometría, es indispensable conocer el concepto intuitivo de punto, recta y plano. Estos son términos no definidos que proveen el inicio de la geometría.

Punto es el objeto fundamental en geometría, el punto representa solo posición y no tiene dimensión, es decir, largo cero, ancho cero y altura cero. Se representan por letras mayúsculas.

Ejemplo:

Tres puntos

Recta tiene solo longitud, no tiene ancho ni altura ni grosor. Es un conjunto infinito de puntos que se extienden en una dimensión en ambas direcciones. Una recta se puede representar por:

Semirrecta la definimos como la porción de una recta que tiene principio pero no tiene fin.

segmento de recta es una porción de la recta con principio y con fin, es decir sabemos donde empieza y donde termina por ende lo podemos medir.

Plano tiene ancho y largo, sin altura ni grosor. Un plano es una superficie en dos dimensiones, se puede pensar como un conjunto de puntos infinitos en dos dimensiones.

En la siguiente aplicación, mueve y manipula los elementos básicos en el plano. Indica cuales de los elementos presentes son puntos, cuales son rectas, cuales son semirrectas y cuales son segmentos.

Ángulos

Un ángulo es la abertura formada por dos rayos que parten de un punto común llamado vértice. 

MEDIDA DE ANGULOS 

Los ángulos se pueden medir en grados. Hay 360 grados en una vuelta completa (un círculo completo). (También se pueden medir ángulos en radianes)

(Nota: "grados" también pueden ser de temperatura, pero aquí sólo hablamos de ángulos)

El símbolo de grado: °

Se usa un pequeño círculo ° después del número para indicar grados.

Por ejemplo 90° significa 90 grados

Un grado

Así de grande es 1 grado

Un círculo completo Un cículo completo son 360° Medio círculo son 180° (esto se llama ángulo llano) Un cuarto de círculo son 90° (y se llama ángulo recto)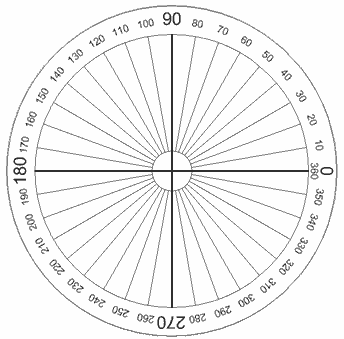

¿Por qué son 360? Probablemente porque antiguamente había calendarios (por ejemplo el persa) que tenían 360 días por año, así que cuando miraban las estrellas veían que giraban alrededor de la Estrella Polar un grado cada día.

Midiendo grados

Muchas veces medimos grados usando un transportador:

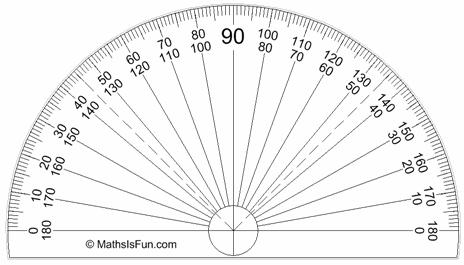
Normalmente los transportadores miden ángulos de 0° a 180°

También hay transportadores de vuelta completa. Pero no son tan comunes porque son grandes y no valen para nada especial.

 
Los tipos de ángulos son: Agudo < 90°
Recto = 90°
Obtuso > 90°
Convexo < 180°
Llano = 180°
Cóncavo > 180°
Completo = 360°
Nulo = 0ºHoy hablaremos de los ángulos agudo, recto y obstuso.

 

2- Tipos de ángulos según su medida
 

Agudo < 90°	Recto = 90°	Obtuso>90°

 


2.1- Ángulos rectos
Un ángulo recto es un ángulo que mide exactamente 90°. Si te das cuenta, en la esquina del ángulo hay unsímbolo especial, una caja. Si ves ese símbolo, el ángulo es recto. No se suele escribir el 90°. Si ves la cajaen la esquina ya te están diciendo que es un ángulo recto.

Un ángulo recto puede estar en cualquier orientación o giro, lo que importa es que el ángulo interior sea 90°

2.2- Ángulos agudos
Un ángulo agudo es un ángulo que mide menos de 90°.

 

Acuérdate de fijarte en cuál de los dos ángulos es al que se refiere uno. Si el ángulo pequeño es menor que90° entonces ese es agudo.

2.3- Ángulos obtusos
Un ángulo obtuso es un ángulo que mide más de 90° pero menos de 180°.

 

Acuérdate de fijarte en cuál de las dos partes es a la que se refiere uno. El ángulo más pequeño entre laslíneas es obtuso si mide entre 90° y 180°.



3- Algunas cosas importantes que debes saber
-Los ángulos que miden 180° se denominan ángulos extendidos o llanos.

- Los ángulos que miden más de 180° y menos de 360° se denominan ángulos cóncavos.

- Los ángulos que miden 360° se denominan ángulos completos.

- El ángulo nulo está formado por dos semirrectas coincidentes, por lo que su abertura es nula, es decir, 0°.

 

- Los ángulos pueden nombrarse utilizando letras griegas. Por ejemplo:

 

 

Ángulos complementarios

Dos ángulos son complementarios si suman 90 grados (un ángulo recto).

Estos dos ángulos (40° y 50°) son ángulos complementarios, porque suman 90°. Fíjate en que juntos hacen un ángulo recto.
Pero los ángulos no tienen por qué estar juntos. Estos dos son complementarios porque 27° + 63° = 90°	Ángulos suplementarios Dos angulos son suplementarios si suman 180 grados. Estos dos ángulos (140° y 40°) son ángulos suplementarios, porque suman 180°. Fíjate en que al ponerlos juntos tenemos un ángulo llano.     Pero no hace falta que los ángulos estén juntos. Estos dos son suplementarios porque 60° + 120° = 180°

RECTAS PARALELAS

Se denominan rectas paralelas a las líneas que mantienen una equidistancia entre sí, y que, aunque prolonguemos su trayectoria hasta el infinito, nunca, en ningún punto sus trazos pueden bifurcarse, tocarse, encontrarse. Es decir, entre ambas líneas (aunque pueden ser planos lineales de mayor dimensión, como ya veremos) se establece una relación de paralelismo.

DEFINICIONES Y TEOREMAS SOBRE RECTAS PARALELAS

DEFINICIONES

- ANGULOS ALTERNOS INTERNOS: Son dos ángulos interiores con diferentes vertices en lados opuestos de la transversal.
- ANGULOS ALTERNOS EXTERNOS: Son dos ángulos exteriores con diferentes vertices en lados opuestos de la transversal.

- ANGULOS CORRESPONDIENTES: Los angulos correspondientes estan en el mismo lado de la transversal. Uno de los angulos es un angulo exterior, el otro es un angulo interior.

TEOREMAS

1. Si dos rectas se cortan por una transversal y un par de ángulos correspondientes son congruentes, entonces las rectas son paralelas.
2. Si dos rectas se cortan por una transversal y un par de ángulos alternos interiores son congruentes, entonces las rectas son paralelas.
3. Si dos rectas se cortan por una transversal y un par de ángulos alternos exteriores son congruentes, entonces las rectas son paralelas. correspondientes
4. Si dos rectas se cortan por una transversal, y un par de ángulos interiores del mismo lado de la transversal son suplementarios, entonces las rectas son paralelas.
5. Dadas las rectas p,q y r, si p ll q y q ll r, entonces p ll r.
6. Si dos rectas paralelas se cortan por una transversal, entonces los ángulos alternos interiores son congruentes.
7. Si dos rectas paralelas se cortan por una transversal, entonces los ángulos alternos exteriores son congruentes.
8. Si dos rectas paralelas se cortan por una transversal, entonces los ángulos son congruentes.
9. Si dos rectas paralelas se cortan por una transversal, entonces los ángulos interiores del mismo lado de la transversal son suplementarios. 

Rectas Perpendiculares

• 

Rectas perpendiculares son las que al cortarse forman cuatro ángulos iguales.
Las rectas m y n son perpendiculares porque al cortarse forman 4 ángulos de 90º.

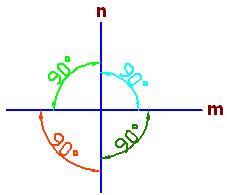
Teoremas

• Teorema: En un plano, dos rectas perpendiculares a una tercera son paralelas.
• Teorema: En un plano dado y por un punto dado de una recta dada, pasa una y solamente una recta perpendicular a la recta dada.
• Teorema de la mediatriz: En un plano dado, la mediatriz de un segmento es la recta perpendicular al segmento en su punto medio.
• Teorema: Desde un punto externo dado, hay a lo menos una recta perpendicular a la recta dada.

COLORARIO: Ningún Triángulo tiene dos Ángulos rectos.

• Teorema - Si B y C equidistan de P y Q entonces todo punto entre B y C también equidistan de P y Q.

COROLARIO: Se da un segmento AB (con raya arriba) y la recta L en el mismo plano. Si dos puntos de L equidistan de A y B, entonces la mediatriz de AB (con raya arriba).

• Teorema - Si una recta es perpendicular a dos rectas que se intersecan en su Punto de intersección, entonces es perpendicular al plano que contiene a las rectas.

RECTAS OBLICUAS

Una recta oblicua es aquella que, al intersecar otra recta, crea un ángulo que no mide 90º (es decir, no se trata de un ángulo recto). Los ángulos creados por las rectas oblicuas, por otra parte, no son iguales (no miden lo mismo).

Ángulos determinado por Rectas Paralelas cortadas po una Secante

• 

Observa en el dibujo que dos rectas paralelas cortadas una recta transversal crea 8 ángulos que reciben distintos nombres según la posición que ocupan:

Las recta r corta a las rectas paralelas m y n:

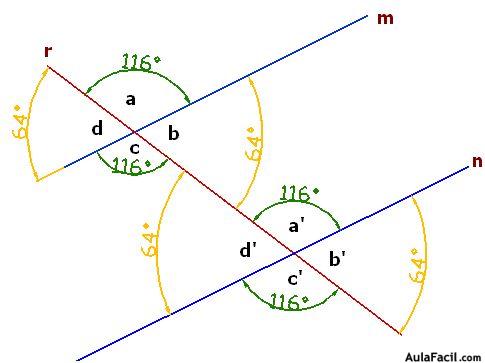
Los nombres de los ángulos según el lugar que ocupan reciben los nombres:

Interiores o internos:

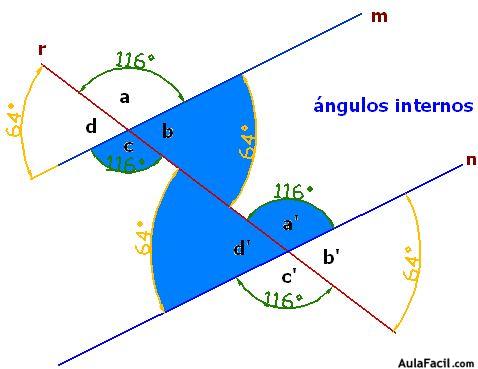
En azul, son los que se encuentran entre las rectas paralelas.

Ángulos exteriores o externos:

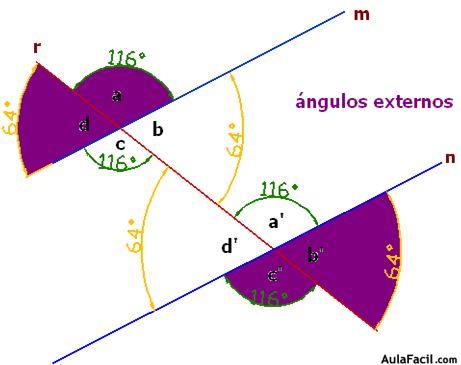
Los ángulos exteriores o externos en color violeta, son los que hallan en la zona exterior de las paralelas.

Ángulos correspondientes:
Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.

Los ángulos del mismo color son correspondientes:

El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’

Teniendo en cuenta lo dicho hasta aquí y fijándonos en la figura podemos afirmar que los ángulos correspondientes son iguales entre sí.

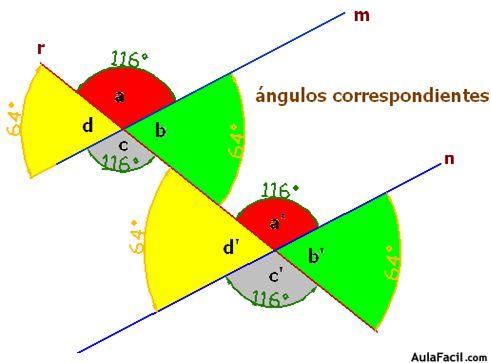
Ángulos alternos internos

Son los que se encuentran a distinto lado de la secante y en la zona interior de las rectas paralelas:

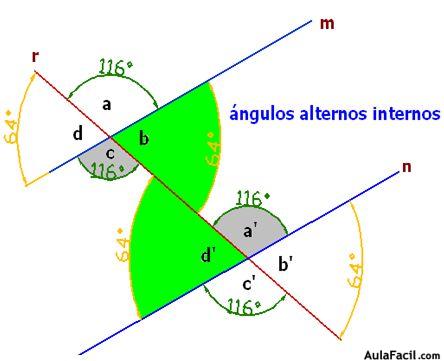
Los ángulos internos son d’, c, b y a’. Si los tomamos alternadamente, tendríamos, por un lado, los ángulos d’ y b, y por otro, c y a’ y comprobarás que los alternos internos son iguales entre sí.

Ángulos alternos externos:

Son los que se encuentran a distinto lado de la secante y en la zona externa de las rectas paralelas:

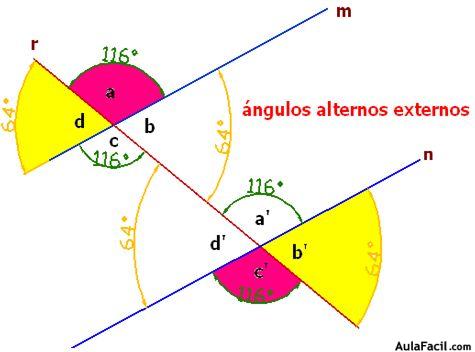
Los ángulos externos son: a, b’, c’ y d que tomándolos alternadamente tendremos, por un lado los ángulos a y c’, y por otro, los ángulos b’ y d. Comprobarás que los ángulos alternos externos son iguales entre sí.

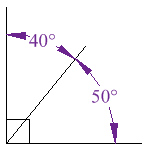
15.55 Observa la figura siguiente y después, contesta a las preguntas siguientes:

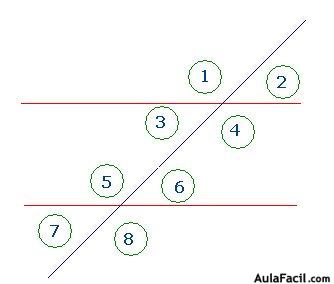
1. ¿Cómo son los ángulos 1 y 2?
2. ¿Cómo podemos llamar a los ángulos 1 y 4?
3. ¿Son suplementarios los ángulos 2 y 4?
4. ¿Son iguales los ángulos 2 y 3? ¿Por qué?
5. ¿Son correspondientes los ángulos 3 y 7?
6. ¿Cómo son los ángulos 4 y 6?
7. ¿Es el ángulo 6 correspondiente al ángulo 3?
8. ¿Son iguales los ángulos 5 y 8? ¿Por qué?
9. ¿Cómo puedes llamarles a los ángulos 1 y 8?
10. ¿Son alternos internos los ángulos 5 y 6?

Respuestas:

1. Adyacentes y suplementarios.
2. Opuestos por el vértice. Uno es externo y el otro interno.
3. Sí, juntos valen 180º.
4. Sí, por ser opuestos por el vértice.
5. Sí por encontrarse en el mismo lado de la secante, siendo uno un ángulo interior y el otro un ángulo exterior.
6. Se encuentren en el mismo lado de la secante, los dos son ángulos interiores.
7. No porque no están situados al mismo lado de la secante y además, los dos son interiores.
8. Sí por estar opuestos por el vértice.
9. Son ángulos alternos externos ya que se encuentran a distinto lado de la secante y en la parte exterior de las paralelas.
10. No porque no son alternos y además, los alternos internos son iguales entre sí.